ENTS,

   Problem #8 is attached. It represents a brief change of pace and hopefully will stimulate interest in volumes. I'll go back to more conventional problems for #9.

Bob 

Problem #8: A white pine has a base radius of 1.75 feet and a total height of 145 feet. From outward appearances, the trunk looks very conical in shape. A cone with a base radius of 1.75 feet and a height of 145 feet would have a volume of 465 cubic feet. Above the base, the measurer is able to get diameter measurements using a Dendrometer for heights up to 105 feet before limbs and foliage obscures the trunk above that height. How high up the trunk must the measurer go to reach 97% of the trunk volume, assuming a conical shape from bottom to top with the radius of the base and the height as given above?

Solution: The diagram and definitions below shows the cone shape and variables needed to solve the problem.

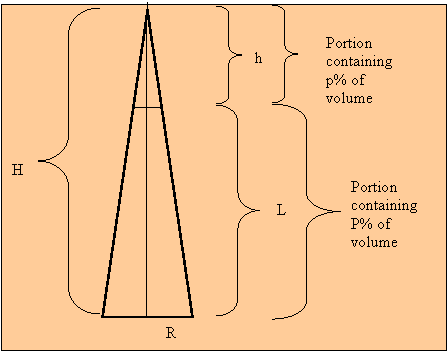
Definitions:

R = radius of base of cone

H = total height of cone

V = total volume of cone

P = specified percentage of total volume calculated from base upward

V_P = actual volume corresponding to percentage P

p = percentage of the remainder of the total volume

h = height from top down at which percentage p is reached

L = height above base at which percentage P is reached

Formulas:

Substitutions & calculations:

            H = 145

            R = 1.75

            P = 0.97

Comments: This problem illustrates how much of the volume of a cone is concentrated in the lower portion. For the tree of this problem, at 29.91 feet above the base, 50% of the volume of the entire trunk has been reached. This is not intuitively obvious, but it is true so long as the shape of the tree in the example is that of a cone. A more challenging problem is to calculate heights and percentages where volumes are reached when the shape is not conical.