ENTS,

   Problem #4 is attached. I won't repeat it here.  I have many problems in mind that can be used to build the bank of solved problems, but I'd rather take suggestions from those of you who want to see certain kinds of problems addressed and solved.

   Also, t he bank isn't just for me to provide input. A good dozen or more of you out there can think up excellent problems and present their solutions to the benefit of all.

Bob 

Problem#4: A tree stands in the middle of the south end of a flat parking lot. The parking lot slants downward from north to south at the rate of a 1 foot drop for every 25 feet of horizontal distance. The high point of the tree is 100 vertical feet above the base and has a horizontal offset of 10 feet in the direction of north. A measurer sets out to measure the tree with a tape and clinometer in the middle of the north end of the parking lot. The measurer’s eye is 6 feet directly above the ground. The measurer lays out a 100 foot baseline to the trunk of the tree. Unbeknownst to the measurer, the clinometer is out of calibration and reads high. Positioned at the end of the 100-foot baseline, the measurer reads the clinometer. He then makes a quick calculation and adds the height of his eye above the base of the tree and pronounces the tree as 114 feet in height. If the measurer is unaware of the horizontal offset when he computes the tree’s height, by how much is his clinometer off?

Solution: This problem needs a diagram. We begin with the following.

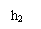
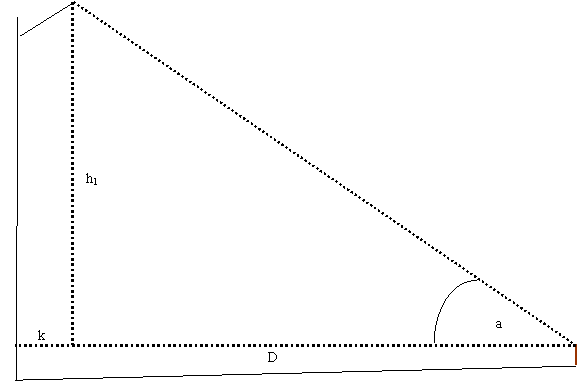
 Where:

            D =100 = baseline to tree

            k = 10 = horizontal offset of high point from trunk

            h₂ = (4 + 6) = 10 = height of tree below eye level

            h₁ = 90 = height of tree above eye level

            The measurer begins by calculating the drop of the parking lot as (1/25)100 = 4 feet and then adds his height to get the part of the trunk below eye level. He does not need to use the clinometer for the below eye level part of the tree’s height. His addition gives him 10 feet. He can now concentrate on height above eye level. If he announces the total height of the tree aa 114 feet, he would have determined 104 feet were above eye level. Since by our initial assumption, he does not know of the horizontal offset or the amount that his clinometer is off, he obviously cannot calculate the true height of the tree.   From the statement of the problem, can we determine the amount off his clinometer is? First we calculate the actual angle from eye to high point. Since the tree is 100 feet tall by our initial assumption and 10 feet are below eye level, the height above eye level is actually 90 feet. In addition, the baseline to the point beneath the high crown-point is actually 100-10=90 feet (adjusting for the horizontal offset). We can determine angle a using the arctangent function.

            This is the actual angle from the measurer’s eye to the top of the tree, but not what he reads on his clinometer. Since his final calculation for the tree’s height is 114 feet and 10 feet are below eye level, we have 104 feet of height that he calculates to be above eye level. Using this information, we can calculate the angle necessary to yield the 104-foot above eye level height using his 100-foot baseline.

            Finally, we calculate the amount off that the clinometer reads.

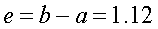
             Our friend’s clinometer reads high by 1.12 degrees. Had the clinometer read accurately, our measurer would have read 45 degrees and the height he would have calculated for the tree using a 100-foot baseline would have been 100 feet above eye level. Adding the10 feet of height below eye level, he would have declared the tree to be 110.0 feet in height instead of 114. His calculations suffer from two sources of error. According to Dr. Lee Frelich, the user fell prey to the combination of Type I and Type II measurement errors.

Summary: This problem illustrates the value of being able to calculate the source and impact of different types of errors. While the mathematics involved is often very basic, our experience shows us that the impacts of various sources of measurement error are often not understood even by experienced measurers.