ENTS,

Attached is the first problem that I promised. It deals with determining trunk length of a leaning tree and is presented in a Word document. The solution  utilizes the law of cosines. Incidentally, Paul Jost has been a good advocate of that law. Maybe we can think up a problem or two.

Bob 

Problem#1: A leaning tree is to be measured from within the plane of the lean, i.e. the tree leans directly toward or away from the measurer. The trunk is straight from ground level to the branching point. The measurer has a clinometer and laser rangefinder. Assume that the distance from the measurer to the top of the trunk is 65 feet at an angle above the eye of 20 degrees. Further assume that the distance from the measurer to the bottom of the trunk is 70 feet at an angle below the eye of 15 degrees. What is the length of the trunk segment?

Solution: The solution involves the law of cosines. A triangle is formed from the eye to the top of the trunk, then down along the trunk to the bottom, and then back to the ey. The triangle must be solved for the distance down the trunk (trunk length) using the distances from the eye to the extremities and the intervening angle.  The figure below depicts the problem. Drawing is not to scale

Let:

D₁ = distance from eye to top of trunk = 65 ft

D₂ = distance from eye to bottom of trunk = 70 ft

A  = angle between D₁ and D₂ = 20+15 = 35

D₃ = distance along the trunk, i.e. trunk length, to be determined

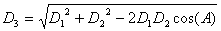     Law of Cosines

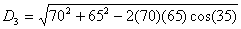
D₃=40.9 feet