Problem #17: This problem deals with the calculation of an area created by the outline of the crown of a tree that is projected downward onto a horizontal plane. We may call the outline thus created the vertical projection of the outline of the crown onto a horizontal plane. Practically speaking, one walks the boundary of the projection, looking for the outward limits of the horizontal projection of the crown, noting where the boundary falls on the ground and marking spots for measurement. The problem is how to implement this concept and more specifically calculate the area included within the boundary.

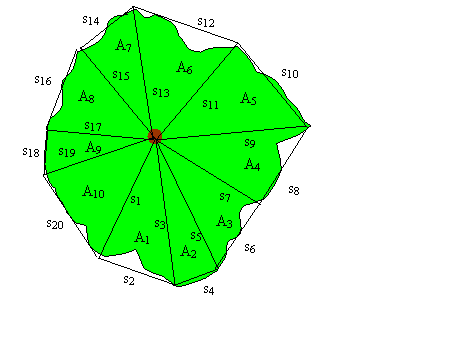
Solution: We can think of the area to be calculated as the shadow of the crown with the sun directly overhead. The shadow creates an image on the ground that can be traced by walking beneath the fartherest limb projections going around the tree. The actual path is continuous and highly irregular, but in practice, the boundary may be approximated by a many-sided polygon. To calculate the area of the polygon, the measurer needs a laser rangefinder, a clinometer, some orange flagging, and 3 stakes approximately head high. Orange (or the measurer’s color preference) flagging is put at the top of each stake for visibility. The measurer positions himself/herself at the end of a conspicuous limb projection and puts one of the stakes in the ground, marking the starting point. Orange flagging is put around the trunk of the tree at a set height above the base. The flagging should follow a level path. The circumference of the tree is measured and the diameter and radius of the trunk calculated. The measurer then goes back to the first stake and moves around the crown to a second point that incorporates the crown’s ground trace fairly faithfully and marks the location with a second stake and then returns to the first stake. Using the laser, the measurer shoots the distance and angle from the first stake to the flag around the tree – aiming for the center of the tree, and records the distance and angle measurements. From the first stake, the measurer then shoots the distance and angle to the top of the second stake and records those measurements. The measurer moves to the second stake and shoots the distance and angle to the trunk, always aiming for the center and records the two measurements. These measurements form the measurer’s first triangle. Its vertex is the center of the trunk. The measurer then takes the third stake and moves beyond the second stake to another point at the end of the outward crown projection and puts the stake in the ground. The measurer shoots the distance and angle back to the second stake and also the distance and angle to the flag around the trunk of the tree and records the measurements. These measurements allow the measurer to form a second triangle adjacent to the first. The measurer retrieves the second stake and bypasses the third stake, finding another point of outward crown projection and puts the second stake in the ground. The measurer then shoots back to the third stake, recording the distance and angle and then shoots to the trunk, recording the distance and angle – always shooting the flagging and aiming at the center of the trunk. A third triangle is formed adjacent to the second. The measurer retrieves the second stake, bypasses the third and finds another point beneath the crown projection and places the second stake in the ground. This process is repeated over and over as the measurer circles the tree until the crown projection path of the tree is completely navigated. The series of triangles formed by this method are adjacent with their vertices being the center of the trunk. From the described measurement set, the polygonal area enclosed within the crown’s ground trace can be calculated along with the average crown spread. The following diagram shows the formulas needed. The accompanying Excel workbook automates the process.

Example diagram showing 10 triangles

Definitions

s_i=distance from eye to trunk or stake

a_i=slope angle of s_i to a stake or the center of the trunk at a set height

S_i=length of a side of a triangle, includes radius of trunk when shooting from a stake to the trunk.

A_j=area of a triangle

A=area of all triangles

S=semi-perimeter of a triangle

P=perimeter of the crown projection onto a horizontal plane

R=radius of trunk

Formulas

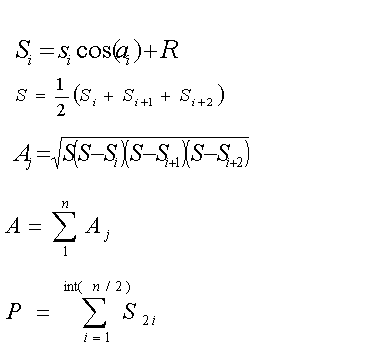
Summary Comments: The above method can be criticized on several grounds. First if the crown trace is on irregular ground and has many obstacles to positions directly beneath crown end points, shortcuts will unquestionably be taken and the polygon will not follow the crown trace sufficiently close enough. It may take 20 or more triangles to do justice to the area calculation. Therefore, the procedure can be labor intensive. All triangles must share vertex a vertex that is on the same vertical trunk center line. Shooting from various points around the trunk, it is doubtful that the vertices will all lie on a common vertical line. However, considering the alternatives, the method if taken far enough can give us a good approximation of crown projection area. A byproduct of this area determination is the average crown spread. By taking each of the radii to the center of the trunk, averaging their lengths and doubling the result, we arrive at the average crown spread.

measure/problems/Problem_17.xls